The training data for this project was very straightforward - one column for each question, and another column that states whether the pair was a duplicate (1 is duplicate, 0 is no). There're two things that make this dataset different than the vanilla binary classification problem. First, these are sequential data which means the context of a particular word depends on the preceeding word(s). Second, the sentences have varied lengths so the input data do not have fixed size. Recurrent Neural Net (RNN) is designed to tackle problems with these characteristics, so let's delve into more details about this model.
Choosing the model
No single machine learning/deep learning method is silver bullet, and it's important to compare methods to find the most efficient way to solve the problem. Often times, Natural Language Processing (NLP) is used for semantic/sentiment analysis of text data, this normally means preprocessing the data into a matrix suitable for machine learning algorithm like Random Forest or Naive Bayesian. However, since those ML models don't take word or sentence as input, it is necessary to tokenize the words in the corpus, then convert the data into numerical feature vectors . You end up with a sparse matrix that contains a normalized numerical vector corresponding to word/n-gram frequency using Tf-idf weighting (for more details, see this link). This approach works well with small text data set or a corpus that has consistent content info. A disadvantage of this approach is that when you get test data that contain new words or new n-grams, the tokenized matrix used to train the model would not be applicable because the new words effectively expanded the feature vector space. To get around this issue, word vectors and RNN can be used.
Word vectors
refer to distributed word vectorization that encapsulates the semantics of each word. The dimension for the
vector is fixed, and it corresponds to different semantic categories. For a sentence, we can embed a word vector to each word,
cap the number of words to a given length before feeding it to the RNN model (this will determine the size of the model and numbers
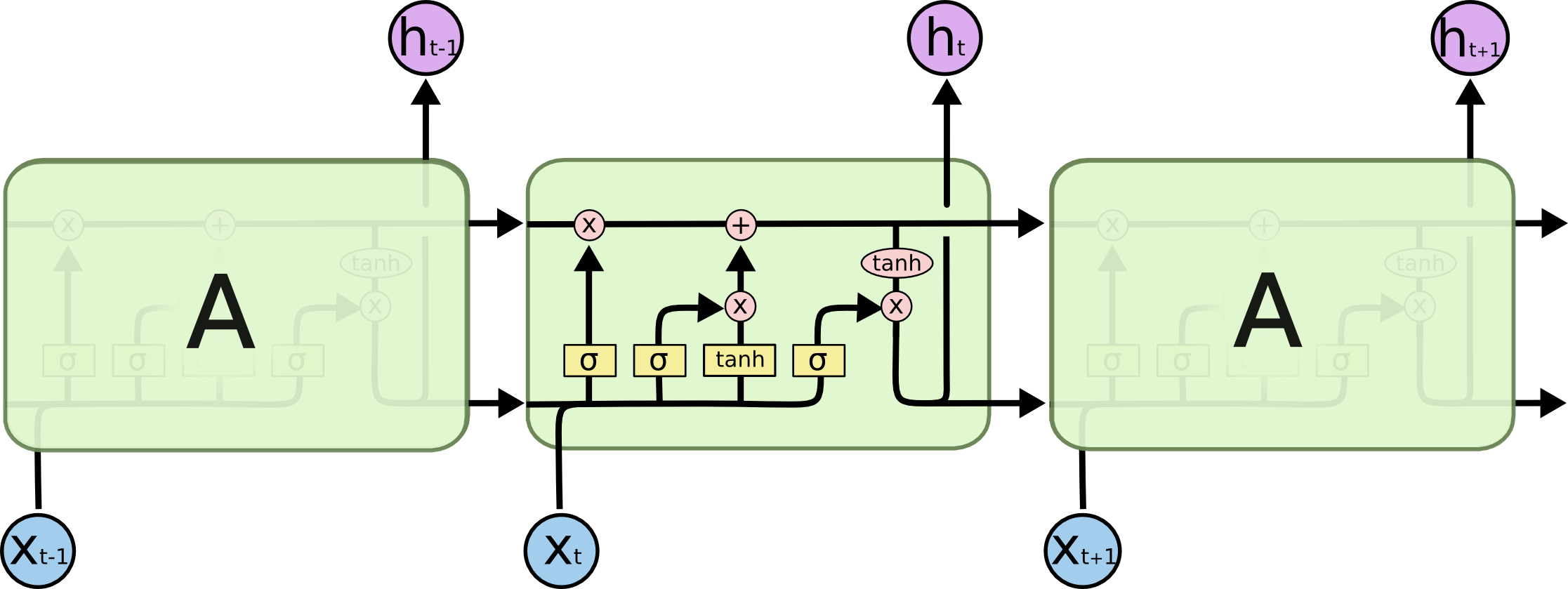
of parameters). Recurrent neural network has chain like structure composed of repeating units, and each unit (after time 0) accepts the data
point AND the output of the previous unit as the input. Long Short Term Memory (LSTM) neural net is a recurrent network with
individual unit that contains a memory cell which runs through the entire chain (see Fig 1 below). This memory cell works with other elements in the unit, such as forget-gate and
input-gate, to decide what information/feature to keep, thus learning the semantic relevance of each word in the case of
sentence input. This architecture allows LSTM to capture information few units prior and the memory
cell avoids the vanishing-gradient problem, which kills off the gradient during backpropagation and diminishes the model's ability to learn.
The down side of using LSTM is the computation cost - the longer the sentence/input, the more parameters the model has to learn.
For instance, a LSTM(128) means for every temporal unit (in this case each word) there's 128 output from the nonlinear
processing of the input using tanh as the activation step.
Implementing LSTM
This code is similar to one of the models suggested in Nikhil Dandekar's blog [1] - the model input would be a pair of questions and it outputs a prediction where 1 is duplicate. Each question is embedded using Stanford's NLP GloVe pretrained word vector, and each embedded vector is fed to a LSTM network [2]. Then the representation output from the LSTM layer is combined to calculate the distance (the sum of the squared difference between the two representation vectors), and that goes through two dense layers with sigmoid functions. This model architecture is similar to Siamese network, except there's the final sigmoid function to predict a binary outcome, and the model is trained by minimizing log loss.
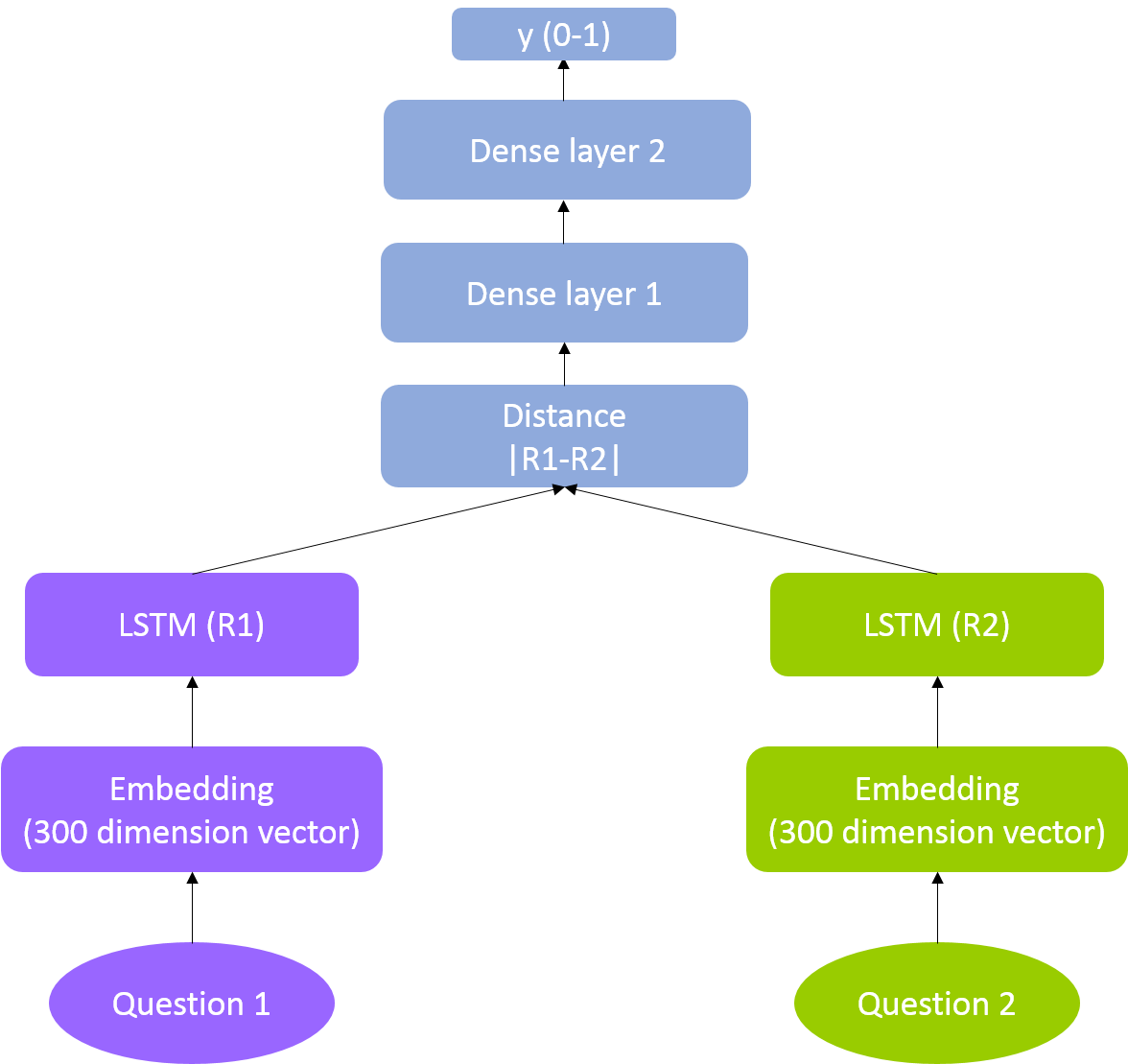
Two codes are shown in my github repository - the first one is the preprocessing step to build the embedding matrix, and the second code is for model training and tuning. In short the LSTM architecture is shown in the code snippet below
#setup the word vector embedding
from keras.layers.embeddings import Embedding
nb_words=137077+1 #unique words in corpus (training and test sets)
max_sentence_len=25
embedding_layer = Embedding(nb_words,300,
weights=[embedding_matrix],
input_length=max_sentence_len,trainable=False)
############# LSTM model using functional API ######################
lstm_layer =LSTM(128)
sequence_1_input = Input(shape=(max_sentence_len,), dtype='int32')
embedded_sequences_1 = embedding_layer(sequence_1_input)
x1 = lstm_layer(embedded_sequences_1)
sequence_2_input = Input(shape=(max_sentence_len,), dtype='int32')
embedded_sequences_2 = embedding_layer(sequence_2_input)
y1 = lstm_layer(embedded_sequences_2)
distance=Lambda(vec_distance, output_shape=vec_output_shape)([x1, y1])
dense1=Dense(16, activation='sigmoid')(distance)
dense1 = Dropout(0.3)(dense1)
bn2 = BatchNormalization()(dense1)
prediction=Dense(1, activation='sigmoid')(bn2)
model = Model(input=[sequence_1_input, sequence_2_input], output=prediction)
Performance
With BatchNormalization() and Dropout(0.3) applied to reduce overfitting,
the LB log loss score was 0.32650. For this project, the number of training data was significantly lower than test data (400K vs. 2M).
Collecting more training data can siginificantly boost model performance, as well as trying pretrained word vectors from different sources.
REFERENCE
[1] Semantic Question Matching with Deep Learning, https://engineering.quora.com/Semantic-Question-Matching-with-Deep-Learning
[2] Using pre-trained word embeddings in a Keras model, https://blog.keras.io/using-pre-trained-word-embeddings-in-a-keras-model.html